Bulk Modulus

The bulk modulus (also called compression modulus) of a substance describes ist resistance to compression. It is defined as the ratio of an infinitesimal pressure increase to the resulting relative decrease of the volume,

B = - V · (∂P / ∂V)_T

where P denotes te hydrostatic pressure, V volume, and ∂P/∂V is the derivative of pressure with respect to volume at constant temperature. The bulk modulus can also be written in terms of density change,

B = ρ · (∂P / ∂ρ)_T

where ρ is the density of the polymer and ∂P/∂ρ is the derivative of pressure with respect to density. The inverse of the bulk modulus is called the compressibility, β,

β = 1 / B

The bulk compression involves only short-range conformational changes whereas shear and tensile forces can cause strong (time-dependent) long-range conformational changes. Hence, the bulk modulus is the only time-independent modulus or, in other words, it is not a viscoelastic but linear elastic property. 

if neighbouring molecules interact only by London dispersion forces (as it is the case for many polymers) then the bulk modulus and the compressibility of a solid are directly related to the Lennard-Jones potential and cohesive energy. For example, for glassy polymers, following relation between the bulk modulus, cohesive energy and molar volume can be derived:¹

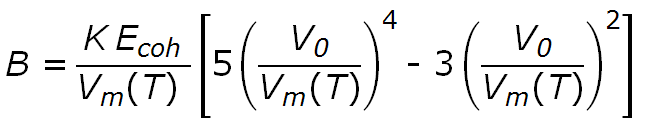
where E_coh is the cohesive energy, V_m(T), V₀ are the molar volume at the chosen temperature T and at zero Kelvin and K is a numerical fitting parameter. Seitz¹ and Bondi² suggested following relationship between the Van der Waals volume and the zero point molar volume of liquid or rubber like polymers: V₀ ≈ 1.3 V_w whereas for polymers in the glassy state Seitz suggested V₀ ≈ 1.4 V_w. The molar volume of a glassy and rubbery polymer can be written as V_m ≈ 1.6 V_w. Using these relations, the bulk elastic modulus becomes

B_am ≈ (9.0 ± 2) E_coh = (9.0 ± 2) δ²

The bulk elastic modulus of polymer crystals is about twice the modulus of glassy polymers, B_cr ≈ 2 B_am and that of rubbery polymers is about half, B_r ≈ 1/2 B_am.

References

1. J.T. Seitz, J. of Appl. Poly. Sci., Vol. 49, 1331-1351 (1993)
2. A. Bondi, Physical Properties of Molecular Crystals, Liquids and Glasses, Wiley, New York, 1968